How to Find Mean of Grouped Data in Excel

Excel Instruction

Finding the Mean of Grouped Data

1.: Make a frequency table in Excel.
2.: Add two new columns: One for the midpoint of each group, and one for the product of the midpoint and the frequency.
3.: Enter the formulas in the two new columns.
4.: Find the sum of the column representing the product of the midpoint and the frequency, and divide this by the sum of the frequency.
Now you have found the mean!

Example 1

A group of skaters are distributed into different weight classes. Here’s a table showing the classes and the frequency of each class.

Weight Frequency
$[115 lb - 125 lb)$ 7
$[125 lb - 135 lb)$ 8
$[135 lb - 145 lb)$ 12
$[145 lb - 155 lb)$ 9
$[155 lb - 165 lb)$ 6

Find the mean weight of this group.

1.

You can see the frequency table of the weight distribution above. The first thing to do is to enter the numbers in Excel.

2.

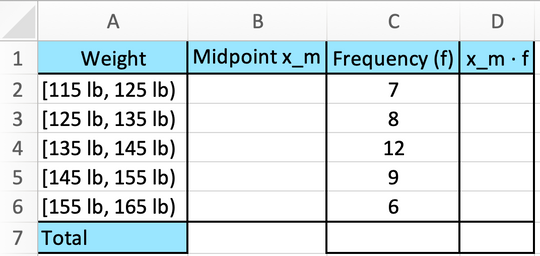
Add the columns “Midpoint

x_{m}

” and “

x_{m} \cdot f

”. The last column is the product of the midpoint and the frequency. Your table should now look like this:

Spreadsheet in Excel presenting frequency table and midpoint column

3.

As you don’t know the exact weight of everyone in the weight class (it could be anywhere between

115

lb-

125

lb,

125

lb-

135

lb, etc.) you have to assume that the weight of everyone in each weight class is in the exact middle. This would be the average of the numbers 115 and 125 for the first, 125 and 135 for the second, and so on.

Write the following formula in cell B2:

=(115+125)/2

Enter the formula for calculating the mean in the remaining weight classes in the column representing the midpoints.

In the “ $x_{m} \cdot f$ ”-column, write the following formula in cell D2:

=B2*C2

Mark cell D2 and copy the formula all the way down to cell D6.

Spreadsheet in Excel showing the formulas used in the calculations

4.